Fluctuation-Dissipation Theorem Meets Score-Based Generative Modeling

The paper Response Theory via Generative Score Modeling has been accepted to Physical Review Letters

The Fluctuation-Dissipation theorem is one of the main results of statistical mechanics. This theorem implies that we can understand (on average) how a system (including nonlinear systems!) responds to a small perturbation just by having knowledge of the unperturbed system. The barrier to applying this theorem is that we need to know the “score function” of the unperturbed system. The score function is the gradient of the system’s log-likelihood. In this work, we show that deep learning can be used to estimate a system’s score function and then to estimate the response function from the fluctuation-dissipation theorem.

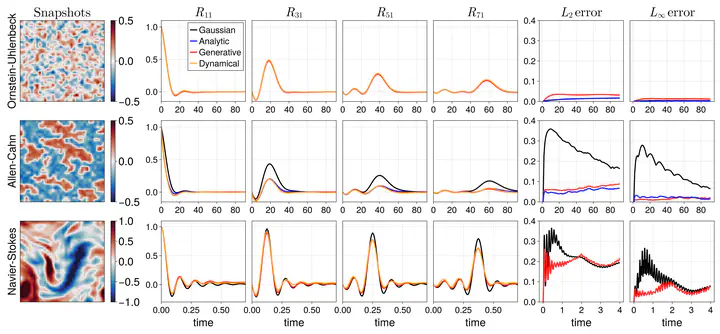
Specifically, the work examines the ability of deep learning to replicate score functions coming from known stochastic dynamical systems and how this can be used to estimate response functions via the fluctuation-dissipation theorem. We examine three stochastic partial differential equations of increasing complexity: a stochastic partial differential equation with Gaussian statistics, a modified Allen-Cahn equation with spatially correlated noise, and the Navier-Stokes equations with hidden dynamics. In all cases we have access to simulations of the original dynamical system and can compare the estimated response functions to the true response functions. We also have access to the analytic score functions in the first two cases. The estimated response functions agree with the true response functions calculated by directly perturbing the dynamical system.

The supplementary material has additional details. We show how to derive the score function, decompose dynamics into reversible on irreversible components (the continuous state space analog of the decomposition in Appendix B of this paper), how to derive the fluctuation-dissipation theorem with state-dependent perturbations, as well as some additional results. In particular, we also show that the score function estimated from data in the modified Allen-Cahn system using deep-learning methods agrees with the analytic score function only when evaluated on data sampled from the same distribution as the training data. The estimated score function is not accurate on data that is dissimilar to the training data. This observation suggests that “operator learning” is only good insofar as the data used to train the operator is representative of the data on which the operator will be used.